Στο πρώτο μέρος του άρθρου είδαμε τους κυριότερους λόγους που ο διάδρομος «δείχνει» αλλά και είναι περισσότερος κουραστικός από το τρέξιμο στο δρόμο. Ωστόσο όπως εύκολα αντιλαμβάνεται κανείς οι περισσότεροι παράγοντες που το καθορίζουν είναι ψυχικοί και εγκεφαλικοί και στη συνέχεια μπορεί κάποιος να διαπιστώσει σε επιμέρους σημεία σωματική επιβάρυνση.

Όμως όλα αυτά είναι λίγο έως πολύ υποκειμενικά. Αυτό που δεν επιδέχεται υποκειμενική κρίση είναι η αξιολόγηση των επιστημών και συγκεκριμένα της φυσικής επιστήμης για το αν είναι ευκολότερο ή δυσκολότερο το τρέξιμο στο διάδρομο.

Κατά γενική ομολογία-πεποίθηση ,οι περισσότεροι δρομείς συμφωνούν ότι το τρέξιμο σε διάδρομο είναι λίγο πιο εύκολο από τον δρόμο. Αλλά αν ισχύει αυτό, πόσο πιο εύκολο; Ένας συνηθισμένος εμπειρικός κανόνας είναι να ρυθμίσετε τον διάδρομο σε κλίση 1-2% για να προσομοιώσετε το τρέξιμο στο έδαφος. Άλλοι επιμένουν ότι είναι προτιμότερο να τρέχεις απλά λίγο πιο γρήγορα για να το αντισταθμίσεις. Ενώ υπάρχουν και εκείνοι που δεν σηκώνουν συζήτηση πιστεύοντας ότι ο διάδρομος απλά κάνει τη δουλειά για εσένα.

 

Η συζήτηση είναι... βαριά για τις εδραιωμένες πεποιθήσεις και τη συμβατική σοφία, αλλά ελαφριά για την πραγματικότητα. Ακόμη και όσοι απουσίαζαν μονίμως από τη τάξη κατά τη παράδοση του μαθήματος της φυσικής στο σχολείο, πλέον με την ενασχόληση τους με το τρέξιμο συχνά πέφτουν πάνω στον κανόνα της κλίσης 1-2% ως μια λογική εξισορρόπηση στις περισσότερες περιπτώσεις. Επίσης διαβάζουν για την εναλλακτική το γρηγορότερου τρεξίματος κατά 3%-6% στον διάδρομο έως μια ακόμη μ επιλογή για την προσομοίωση του τρεξίματος σε εξωτερικό περιβάλλον (δρόμο, στάδιο κτλ).

Σε αυτό το δεύτερο μέρος με τη βοήθεια του επαγγελματία τριαθλητή Cody Beals ο οποίος έχει σπουδάσει Φυσική στο Πανεπιστήμιο Queens των Η.Π.Α, θα προσπαθήσουμε να εμβαθύνουμε λίγο περισσότερο προσπαθώντας –στο βαθμό του εφικτού- να μην φανούμε κουραστικοί κατά την ανάγνωση. Εάν πάλι η φυσική σας έχει αφήσει δυσάρεστες αναμνήσεις, μη διστάσετε να παραλείψετε τις σημειώσεις και εστιάστε στα γραφήματα των αποτελεσμάτων που προκύπτουν από την... αντιπαθή σε κάποιους επιστήμη της φυσικής. Τι να κάνουμε…Το τρέξιμο έκτος από ψυχή, καρδιά και πόδια περιλαμβάνει και άλλες παραμέτρους!

Η επιστήμη της φυσικής μας «μιλάει» για το τρέξιμο

Η φυσική που περιγράφει το τρέξιμο είναι περίπλοκη, ανεξάρτητα από το αν υπάρχει διάδρομος ή όχι, σπεύδει να μας ξεκαθαρίσει εξαρχής ο Βeals. Το σημείο εκκίνησης για οποιοδήποτε πρόβλημα δυναμικής όπως αυτό που αφορά στο τρέξιμο είναι ένα διάγραμμα δυνάμεων, που ονομάζεται διάγραμμα ελεύθερου σώματος. Θα εξετάσουμε έναν δρομέα που κινείται με σταθερή ταχύτητα και ασκείται από τρεις εξωτερικές δυνάμεις: τη δύναμη της βαρύτητας (γνωστή και ως βάρος), την αεροδυναμική δύναμη έλξης (γνωστή και ως αντίσταση αέρα) και τη δύναμη αντίδρασης του εδάφους. Η δύναμη της βαρύτητας είναι σταθερή και θα υποθέσουμε ότι η έλξη είναι επίσης περίπου σταθερή. Ωστόσο, η αντίδραση εδάφους ποικίλλει κατά τη διάρκεια του κύκλου βάδισης.

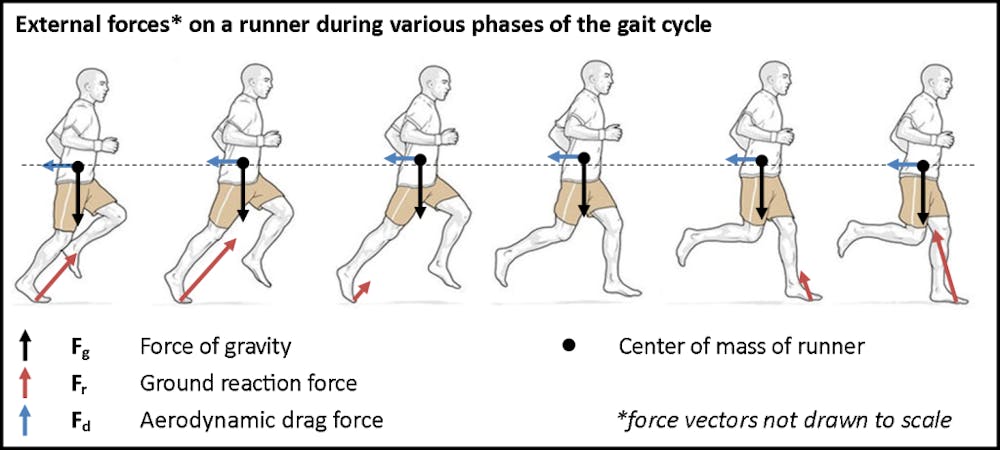
Η δύναμη αντίδρασης του εδάφους αλλάζει συνεχώς σε μέγεθος και κατεύθυνση. Αυξάνεται λίγο μετά το χτύπημα του ποδιού και είναι μηδέν όταν και τα δύο πόδια είναι πάνω από το έδαφος (στον αέρα). Μέρος αυτού που κάνει το τρέξιμο τόσο δύσκολο στη μοντελοποίηση είναι ότι οι δυνάμεις σε έναν δρομέα δεν είναι ποτέ ισορροπημένες, ακόμη και κατά το τρέξιμο με σταθερή ταχύτητα. Ως αποτέλεσμα, το κέντρο μάζας ενός δρομέα πάντα επιταχύνεται, ή πιο συγκεκριμένα, ταλαντώνεται.

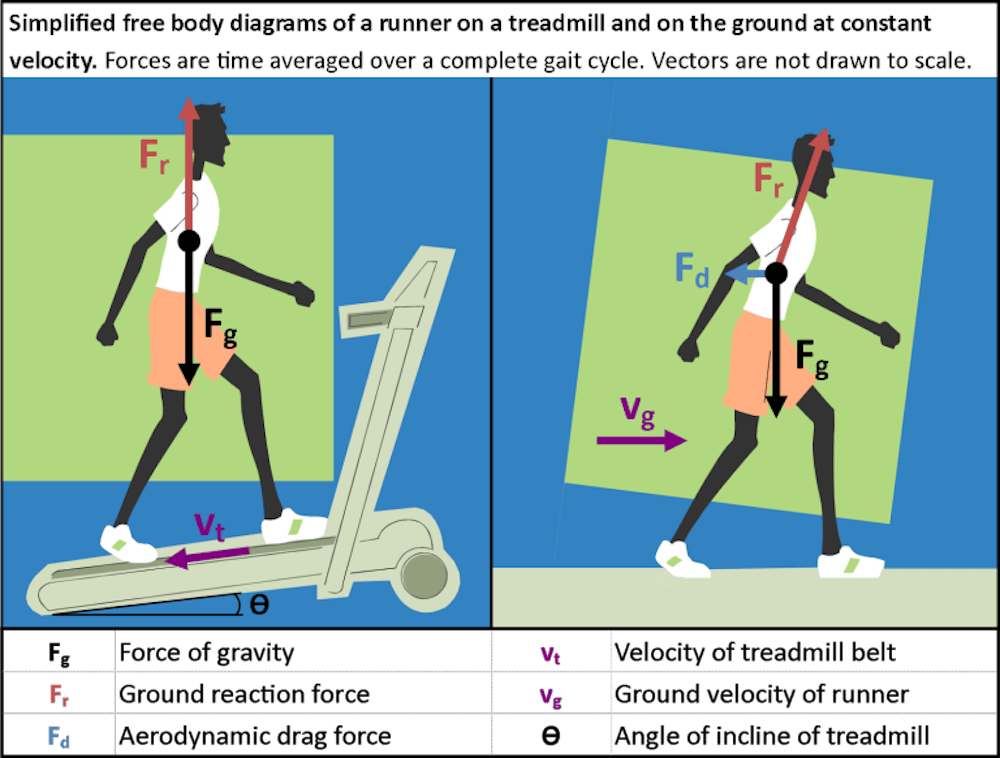
Για να απλοποιήσει αυτό το πρόβλημα, εξέτασε μόνο τις μέσες εξωτερικές δυνάμεις σε έναν πλήρη κύκλο βάδισης και υπέθεσε ότι δρουν στο κέντρο μάζας του δρομέα. Εφόσον ο δρομέας κινείται προς τα εμπρός με σταθερή ταχύτητα, η μέση ισορροπία δυνάμεων, δηλαδή η καθαρή δύναμη στον δρομέα είναι μηδέν. Ακολουθούν τα απλουστευμένα διαγράμματα ελεύθερου σώματος για τρέξιμο σε διάδρομο και στο δρόμο.

Τι γίνεται με την τριβή;

Η δύναμη αντίδρασης του εδάφους (Fr Διάγραμμα 2) συχνά χωρίζεται σε μια κανονική δύναμη κάθετη στην επιφάνεια και μια δύναμη τριβής παράλληλη στην επιφάνεια που ενεργεί στο σημείο επαφής. Η δύναμη τριβής θα μπορούσε να υποδιαιρεθεί περαιτέρω σε στατικές και κινητικές συνιστώσες τριβής, με τα τελευταία να παίζουν ρόλο εάν τα παπούτσια του δρομέα έχουν μεγάλο χρόνο επαφής-τριβής με το έδαφος.

Μια βασική υπόθεση είναι ότι η μόνη σημαντική διαφορά μεταξύ τρεξίματος σε επίπεδο έδαφος και σε οριζόντιο (μη κεκλιμένο) διάδρομο είναι η δύναμη έλξης (Fd). Αυτή η δύναμη υπάρχει μόνο στο κανονικό τρέξιμο (εξωτερικό χώρο), αφού ένας δρομέας σε διάδρομο είναι ακίνητος σε σχέση με τον αέρα (παραμελώντας την κίνηση των άκρων, τα ρεύματα αέρα από τους ανεμιστήρες κ.λπ.).Υπέθεσε επίσης, ότι οι αερόβιες απαιτήσεις και η εμβιομηχανική του τρεξίματος σε διάδρομο είναι κατά τα άλλα ίδιες με το τρέξιμο στο έδαφος.

 

Φυσικά, υπάρχουν πολλοί άλλοι παράγοντες που μπορούν να συμβάλλουν στο να γίνει το τρέξιμο σε εξωτερικούς χώρους πιο δύσκολο από το τρέξιμο σε διάδρομο. Λόφοι, άνεμος, πρόσφυση, καιρός, εμπόδια κ.λπ. Οι συντελεστές μετατροπής που υπολογίστηκαν από τον Βeals  βασίζονται αποκλειστικά στη διαφορά που οφείλεται στην αεροδυναμική αντίσταση (υποθέτοντας συνθήκες ανέμου), και ως εκ τούτου θα πρέπει να θεωρούνται ελάχιστες εκτιμήσεις.

Θεώρησε λοιπόν ως υπόθεση εργασίας ότι ο στόχος είναι να παράγουμε την ίδια απόδοση ισχύος με το τρέξιμο σε επίπεδο έδαφος ρυθμίζοντας τον διάδρομο σε κλίση και διατηρώντας την ίδια ταχύτητα-ρυθμό. Αυτό θα έκαιγε τον ίδιο αριθμό θερμίδων και είναι λογικό να υποτεθεί ότι θα παρέχει ένα παρόμοιο προπονητικό όφελος.

Στη φυσική, μια σταθερή δύναμη (F) λέγεται ότι λειτουργεί (W) σε ένα αντικείμενο όταν το αντικείμενο υφίσταται μια μετατόπιση (d) προς την κατεύθυνση της δύναμης.

Η σταθερή δύναμη βαρύτητας σε έναν δρομέα είναι η μάζα του (m) επί την επιτάχυνση λόγω της βαρύτητας (g).

Ένας κεκλιμένος διάδρομος χαμηλώνει το κέντρο μάζας του δρομέα σε κάθε βήμα. Εκτός από κάθε εργασία που περιλαμβάνει το τρέξιμο σε οριζόντιο διάδρομο, ένας δρομέας σε κεκλιμένο διάδρομο πρέπει να κάνει λίγη επιπλέον εργασία ενάντια στη βαρύτητα σε κάθε βήμα για να ανυψώσει το κέντρο μάζας του και να παραμείνει σχεδόν ακίνητος. Ας υποθέσουμε ότι ένας δρομέας δεν ανακτά καμία από αυτή την ενέργεια (δηλαδή ότι η δυναμική ενέργεια δεν μετατρέπεται ξανά σε χρήσιμη κινητική ενέργεια).

Οι σχέσεις μεταξύ της κλίσης του διαδρόμου και του κανονικού ρυθμού τρεξίματος (Διάγραμμα 3) και της ταχύτητας (Διάγραμμα 4) που προβλέπεται να παράγουν ίση μηχανική ισχύ εξόδου εμφανίζονται παρακάτω. Η σταθερή γραμμή είναι για τον μέσο δρομέα . Δεδομένου ότι οι δρομείς έχουν όλα τα σχήματα και μεγέθη και η πυκνότητα του αέρα μπορεί να ποικίλει αρκετά (με υψόμετρο, θερμοκρασία, πίεση και υγρασία), οι διακεκομμένες γραμμές αντιπροσωπεύουν περιπτώσεις όπου οι συνδυασμοί των παραμέτρων είναι 20% υψηλότεροι ή χαμηλότεροι από τη βασική περίπτωση της υπόθεσης εργασίας.

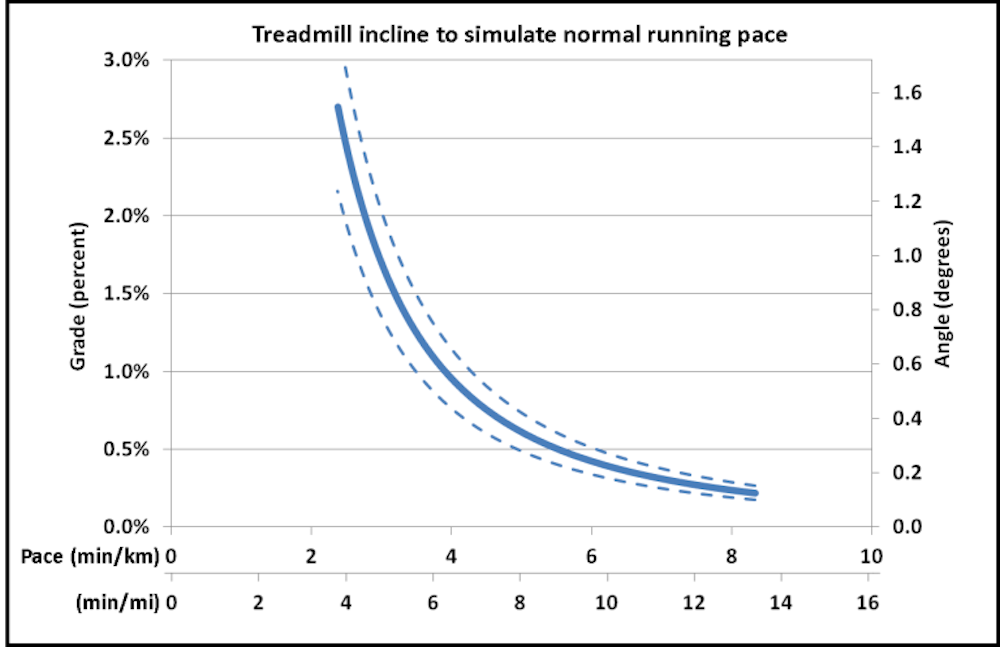
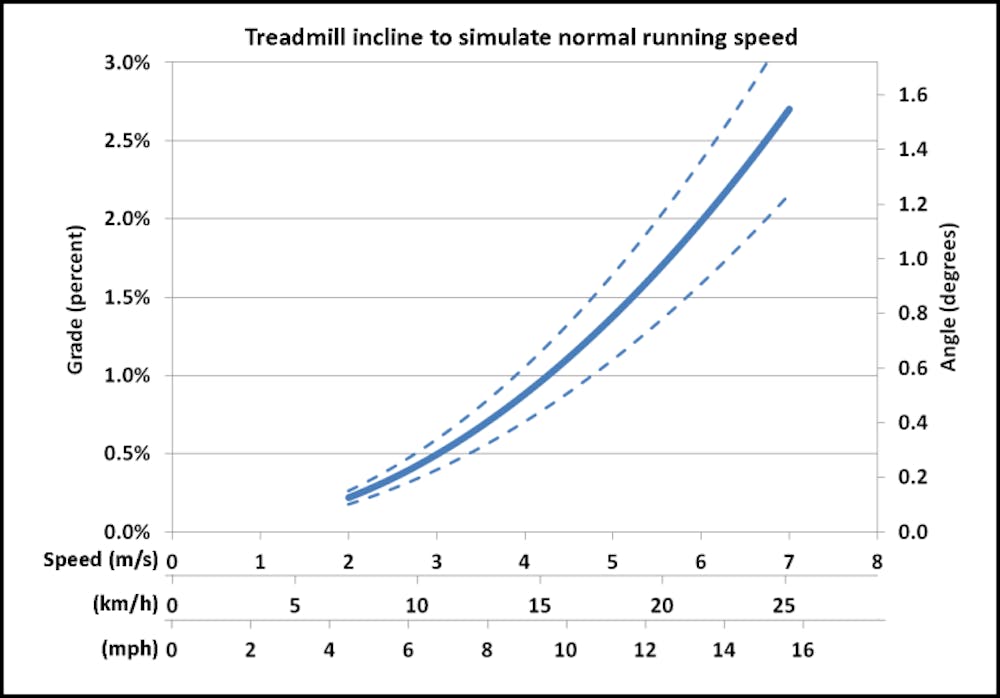
(Η κλίση του διαδρόμου προβλέπεται να παράγει μηχανική ισχύ ισοδύναμη με το τρέξιμο στο έδαφος με τον ίδιο ρυθμό (πάνω) ή ταχύτητα (κάτω). Οι συμπαγείς γραμμές αντιπροσωπεύουν έναν μέσο δρομέα με μάζα 68 kg και CdA 0,6 για την πυκνότητα αέρα στο επίπεδο της θάλασσας (1,225 km/m³). Οι διακεκομμένες γραμμές αντιπροσωπεύουν περιπτώσεις όπου οι συνδυασμοί αυτών των παραμέτρων είναι 20% υψηλότεροι ή χαμηλότεροι από τη βασική περίπτωση)

Συμπέρασμα: Ο εμπειρικός κανόνας κλίσης 1-2% για τρέξιμο σε διάδρομο φαίνεται να είναι αρκετά ακριβής αλλά σε μεγαλύτερες ταχύτητες τρεξίματος (<4:00/km ή >10 mph). Εάν τρέχετε πιο αργά από αυτό, τότε το 1% είναι πιθανώς επαρκές αν όχι και υπερβολικό. Είναι καθησυχαστικό ότι αυτός ο θεωρητικός υπολογισμός συμφωνεί με ορισμένα πειραματικά στοιχεία: Η κλίση διαδρόμου εως 1% αντικατοπτρίζει με μεγαλύτερη ακρίβεια το ενεργειακό κόστος του τρεξίματος σε εξωτερικούς χώρους. 

Η επιλογή της αυξησης της ταχύτητας αντι της κλίσης 

Μερικοί δρομείς και προπονητές ισχυρίζονται ότι το διαρκές τρέξιμο σε κλίση, έστω και ελαφριά, αλλοιώνει την εμβιομηχανική σας. Υποστηρίζουν λοιπόν ότι είναι προτιμότερο να αυξήσεις την ταχύτητά σου για να αντισταθμίσεις. Το ερώτημα είναι πόσο;

Για να βρει μια απάντηση ο Βeals, άφησε πίσω του το βασίλειο της λογικής φυσικής που έχει δεκάδες παραμέτρους.Υπέθεσε ξανά ότι στόχος μας είναι να παράγουμε ίση ισχύ στον διάδρομο όπως στο έδαφος, αλλά αυτή τη φορά αυξάνοντας την ταχύτητά μας και αφήνοντας την κλίση στο μηδέν. 

 

Χρησιμοποιώντας τις ίδιες τιμές όπως πριν, κατέληξε οτι μια ταχύτητα διαδρόμου ~19 km/h (~3:10/km ρυθμός) ισοδυναμεί με μια κανονική ταχύτητα τρεξίματος στο δρόμο ~18 km/h (3:20/km ρυθμός) , που φαίνεται λογικό. Η σχέση για τον μέσο δρομέα σε ένα εύρος ταχυτήτων και ρυθμών παρουσιάζεται παρακάτω. Οι διακεκομμένες γραμμές δείχνουν μια αναλογία 1:1, υποδεικνύοντας ότι η επίδραση της αεροδυναμικής οπισθέλκουσας είναι αρκετά μικρή στις χαμηλές ταχύτητες.

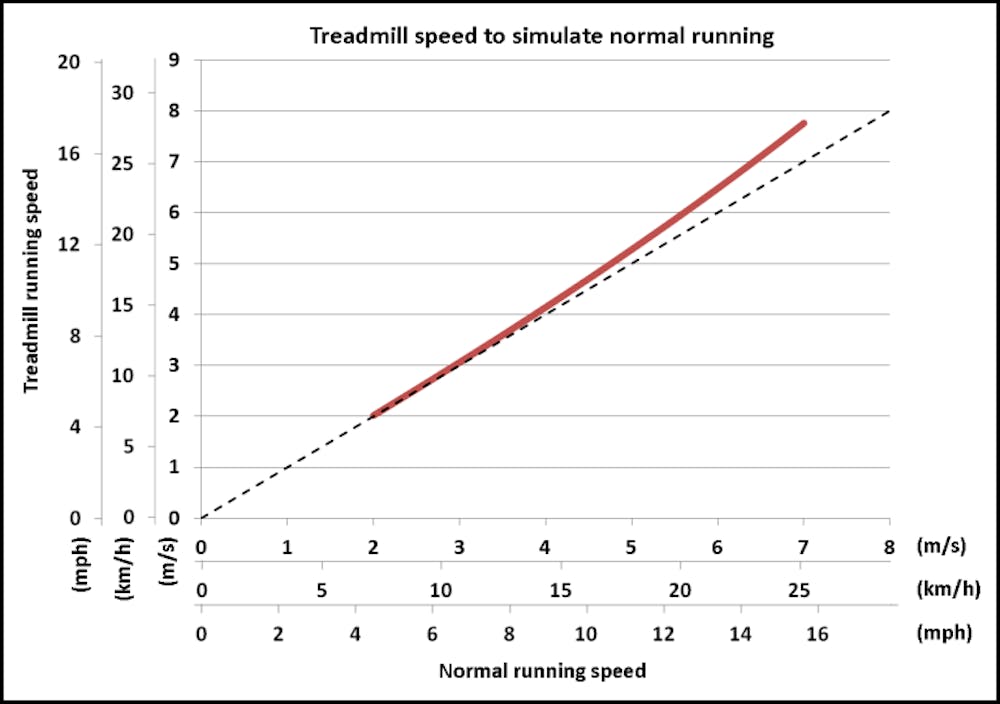
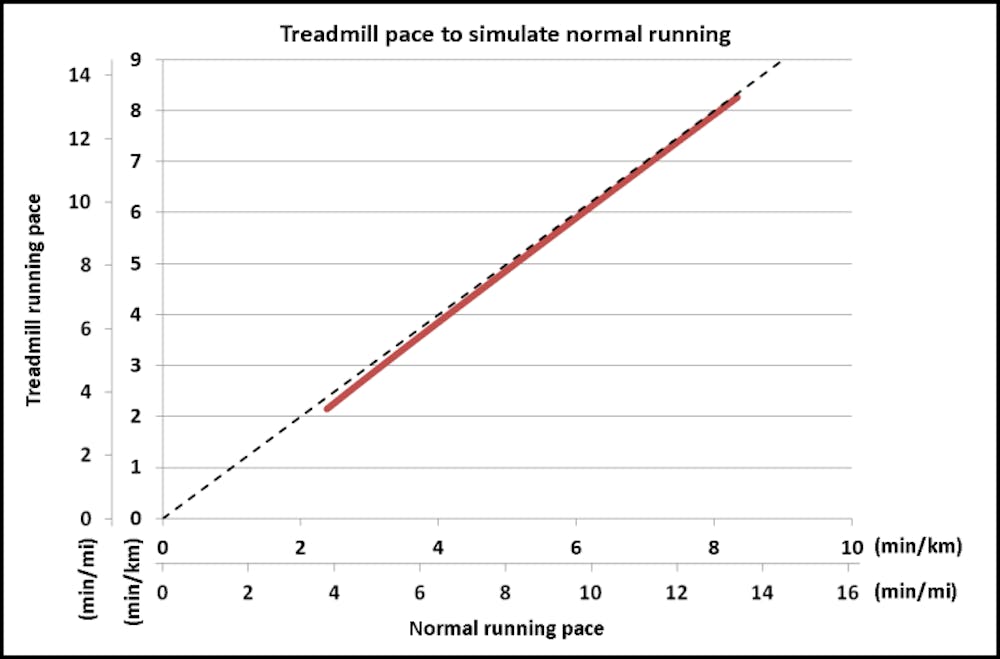
(Οι ταχύτητες τρεξίματος σε διάδρομο και στο δρόμο(Διάγραμμα 5) και ο ρυθμός (Διάγραμμα 6) προβλέπεται ότι θα παράγουν ισοδύναμη μηχανική ισχύ εξόδου. Οι υπολογισμοί βασίζονται σε έναν μέσο δρομέα με μάζα 68 kg (150 lbs) και CdA 0,6 για την πυκνότητα του αέρα στο επίπεδο της θάλασσας (1,225 km/m³). Οι διακεκομμένες γραμμές υποδεικνύουν αναλογία 1:1, δηλαδή καμία αεροδυναμική αντίσταση).

Συμπέρασμα: Αυτό το εξαιρετικά απλουστευμένο μοντέλο προβλέπει ότι πρέπει να τρέχετε 3-6% γρηγορότερα σε μη κεκλιμένο διάδρομο για να προσομοιώσετε ρυθμούς στο έδαφος με pace απο 3:00/km-5:00/km

Ακολουθεί ένας εύχρηστος πίνακας μετατροπών ρυθμού είτε ο διάδρομος που τρέχετε έχει ένδειξη χιλιομέτρων, είτε μιλίων :

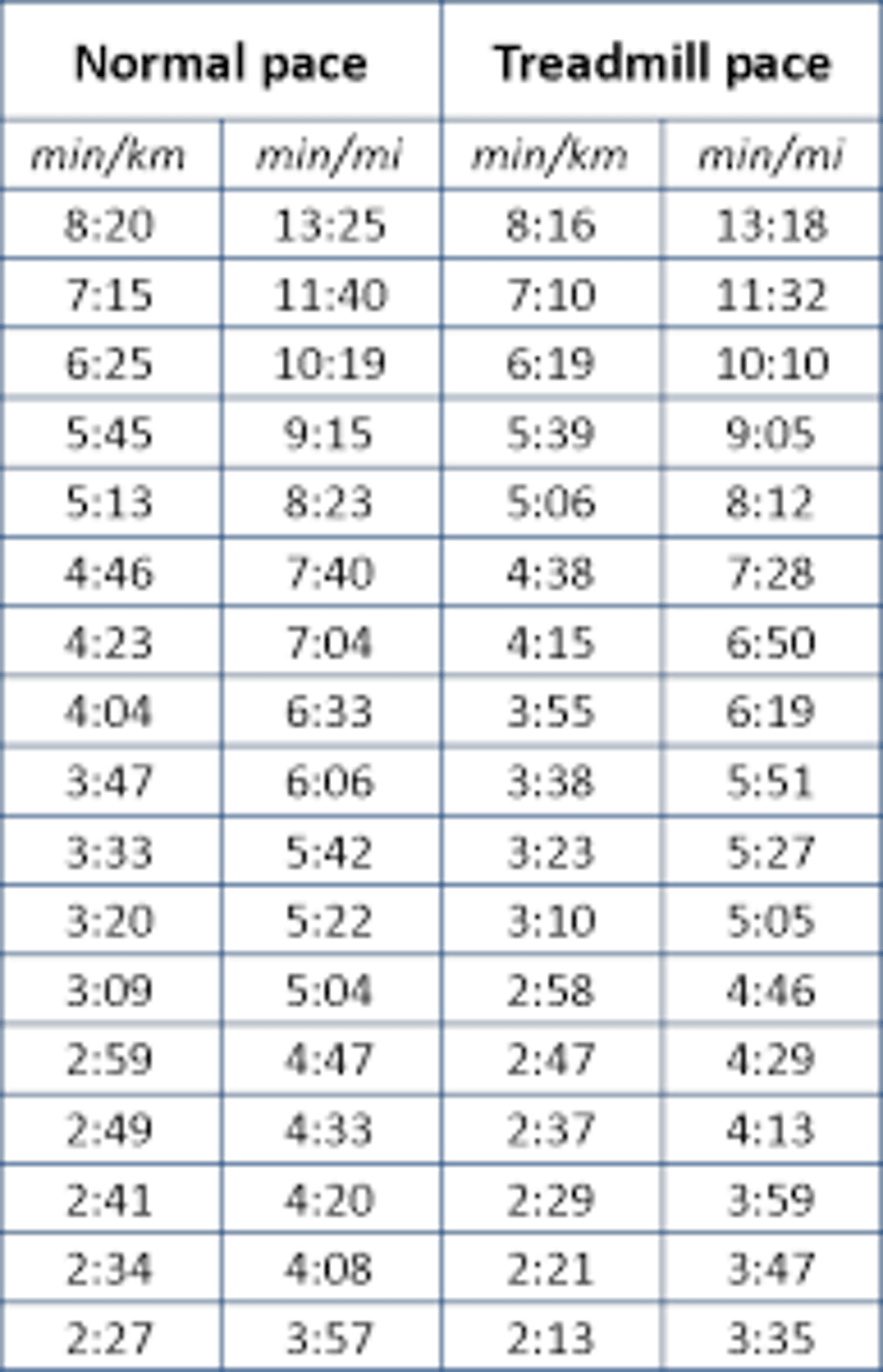
Ποια επιλογή είναι καλύτερη;

Εν ολίγοις, δεν υπάρχει ξεκάθαρη απάντηση. Oτι κι αν επιλέξετε, τρέξιμο σε διάδρομο με κλίση ή τρέξιμο σε διάδρομο με μεγαλύτερη ταχύτητα, -πλέον με τα στοιχεία που σας έχουμε παραθέσει έχετε μια εικόνα για το πως μπορείτε να εξομοιώσετε στο βαθμό του εφικτού το τρέξιμο στο διάδρομο με το τρέξιμο σε εξωτερικό περιβάλλον-,αυτό που έχει σημασία είναι να αξιοποιήσετε κάθε δυνατότητα και επιλογή που έχετε για να ασκηθείτε ανάλογα με τις συνθήκες (καιρικές, καθημερινότητα, υποχρεώσεις, πρόγραμμα κτλ).

Σε κάθε περίπτωση το τρέξιμο σε εξωτερικό περιβάλλον δεν συγκρίνεται με τίποτα. Άλλωστε εμπεριέχει την πεμπτουσία αυτής της μορφής της άθλησης. Την ελευθερία!